[ad_1]
Overview of the study area
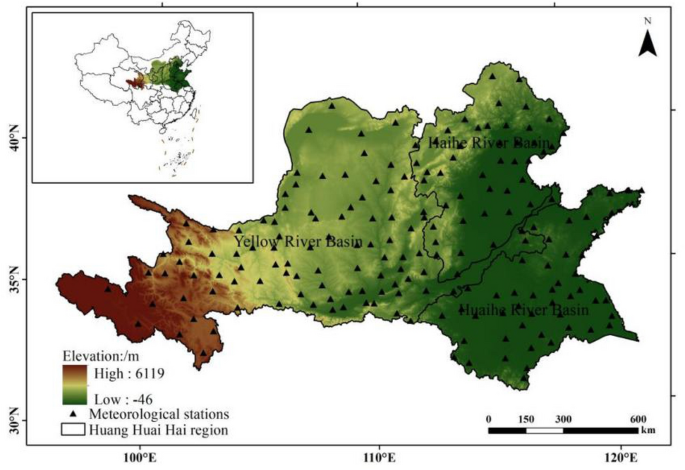
Based on the actual cultivation of peanuts, the Huang-Huai-Hai region is selected as the study area (Fig. 1). The main body of the study area is the Huang-Huai-Hai Plain (North China Plain), which is a typical alluvial plain resulting from extensive sediment deposition carried by the Yellow River, the Huaihe River and the Haihe River and their tributaries, and the hills in central and southern Shandong Peninsula adjacent to it. Administrative zones include 5 provinces, 2 cities, 53 cities and 376 counties (districts). In China, The Huang-Huai-Hai region is an important production and processing centre for agricultural products, with a total land area of 4.10 × 105 square kilometers and cultivated fields of 2.15 × 107 hm2, accounting for 4.3% and 16.3% of the total amount of the country, respectively. It belongs to temperate continental monsoon climate with distinct seasons, accumulated temperature of 3600–4800 degrees above 10 °C, frost-free period of 170–200 days and annual precipitation of 500–950 mm27. The Huang-huai-hai region is the largest peanut growing area, accounting for more than 50% of the country’s peanut production and area28.
Location of the study areas. The figure was made in the ArcGIS 10.2 platform (https://www.esri.com/en-us/home).
Data sources
The data used in the study mainly include meteorological data, geographic information data and crop data. The meteorological data comes from China Meteorological Information Center (http://data.cma.cn), including the daily maximum temperature (℃), daily minimum temperature (℃), daily average temperature (℃), daily precipitation (mm) and daily average wind speed (M/s) observed by 186 ground observation meteorological stations in the Huang-Huai-Hai region from 1960 to 2019 (Fig. 1). Geographic information data include elevation DEM data (resolution of 1 km × 1 km) and land use data in the study area, which are from the resource and environmental science and data center of Chinese Academy of Sciences (http://www.resdc.cn). Crop data, including peanut sowing area and yield data, are derived from the statistical yearbooks of provinces and cities in the study area and China Agricultural Technology Network (http://www.cast.net.cn).
Data processing
Meteorological data processing
Anusplin software is a tool to interpolate multivariate data based on ordinary thin disks and local thin disk spline functions, enabling the introduction of covariates for simultaneous spatial interpolation of multiple surfaces, suitable for meteorological data time series29. First, the Anusplin software is used to spatially interpolate the meteorological data and suitability data of the peanut growing season (April to September) from 1960 to 2019 based on the elevation data with a resolution of 1 km × 1 km. The Inverse Distance Weight (IDW) interpolation can make the meteorological data after Anusplin interpolation maintain consistency with the original data, and is able to improve the interpolation accuracy. Finally, the meteorological and suitability data set with a resolution of 1 km × 1 km is obtained. ArcGIS and MATLAB software were used to count the median of regional meteorological factors in agricultural fields of different cities (counties), and the meteorological factors and suitability of different periods of peanut growth season in each city (county) were obtained.
Yield data processing
Many factors affect crop yield formation, which can be generally divided into three main categories: meteorological conditions, agronomic and technological measures, and stochastic factors. Agricultural technical measures reflect the development level of social production in a certain historical period and become time technology trend output, which is referred to as trend output for short, and meteorological production reflects short period yield components that are affected by meteorological elements. Stochastic factors account for a small proportion and are often ignored in actual calculations30. The specific calculation is as follows:
$$Y={Y}_{t}+{Y}_{w}$$
(1)
where Y is the actual yield (single production) of the crop, Yt is the trend yield, and Yw is the meteorological yield.
In this paper, a straight-line sliding average method is used to simulate the trend yield. The straight-line sliding average method is a very commonly used method to model yield, and it considers the change in the time series of yield within a certain stage as a linear function, showing a straight line, as the stage continuously slides, the straight line continuously changes the position, and the backward slip reflects the continuous change in the evolution trend of the yield history31. The regression models in each stage are obtained in turn, and the mean value of each linear sliding regression simulation value at each time point is taken as its trend yield value. The linear trend equation at some stage is:
$${Y}_{i}left(tright)={a}_{i}+{b}_{i}t$$
(2)
where i = n-k + 1, is the number of equations; k is the sliding step; n is the number of sample sequences; t is the time serial number. Yi(t) is the function value of each equation at point t. there are q function values at point t. the number of q is related to n and k. Calculate the average value of each function value at each point:
$$overline{{Y }_{i}(t)}=frac{1}{q}sum_{j=1}^{q}{Y}_{i}left(tright)$$
(3)
Connecting the (overline{{Y }_{i}(t)}) value of each point can represent the historical evolution trend of production. Its characteristics depend on the value of k. Only when k is large enough, the trend yield can eliminate the influence of short cycle fluctuation. After comparison and considering the length of yield series, k is taken as 5 in this paper.
After the trend yield is obtained, the meteorological yield is calculated using Eq. (1), then the relative meteorological production is
$${Y}_{r}=frac{{Y}_{w}}{{Y}_{t}}$$
(4)
The relative meteorological yield shows that the relative variability of yield fluctuation deviating from the trend, that is, the amplitude of yield fluctuation, is not affected by time and space, and is comparable. However, when the value is negative, it indicates that the meteorological conditions are unfavorable to the overall crop production, and the crop yield reduction, that is, the yield reduction rate32.
Characteristics of spatial and temporal distribution of climatic resources in the Huang-Huai-Hai region
Collect meteorological resource data from 1960 to 2019. Taking 1960–1989 as the first three decades of the study and 1990–2019 as the last three decades, the climatic resource changes of peanut growth in the Huang-Huai-Hai region are analyzed by interpolation of heat resources (average temperature), water resources (precipitation) and light resources (sunshine hours) in the study area in two periods combined with topographic factors.
Establishment of suitability model
According to the definition of phenological time and growth period of peanut planting practice in the Huang-Huai-Hai region, the growth season of peanut is divided into three growth periods and five growth stages (Table 1). Temperature, precipitation and sunshine hours are the necessary meteorological factors to determine the normal development of peanut. Therefore, combined with climatic resources in the study area, temperature, precipitation and sunshine suitability model was introduced to quantitatively analyze the suitability of peanut planting.
Temperature suitability model
Temperature is a very important factor in the growth period of peanut, and the change of temperature in different growth periods will have a great influence on the yield and quality of peanut. As a warm-loving crop, accumulated temperature plays a decisive role in the budding condition and nutrient growth stage of peanut. Temperature determines the quality of fruit and the final yield of peanut. Beta function33 is used to calculate temperature suitability, which is universal for crop-temperature relationship. The specific calculation is as follows:
$${F}_{i}left(tright)=frac{(t-{t}_{1}){({t}_{h}-t)}^{B}}{({t}_{0}-{t}_{1}){({t}_{h}-{t}_{0})}^{B}}$$
(5)
where the value of B is shown in
$$B=frac{{t}_{h}-{t}_{0}}{{t}_{0}-{t}_{1}}$$
(6)
where Fi(t) is the temperature suitability of a certain growth period; t is the daily average temperature of peanut at a certain development stage; t1, th and t0 are the lower limit temperature, upper limit temperature and appropriate temperature required for each growth period of peanut. Refer to the corresponding index system and combined with the peanut production practice in Huang-Huai-Hai region34,35,36, determine the three base point temperature of peanut in each growth period, as shown in the Table 2.
Precipitation suitability model
Peanut has a long growth period, which is nearly half a year. Insufficient or excessive water during the growth period has a great impact on the growth and development, pod yield and quality of peanut. Combined with the actual situation of Huang-Huai-Hai region and peanut precipitation / water demand index, the water suitability function is determined and calculated as follows:
$${text{F}}_{{text{i}}} left( {text{r}} right) = left{ {begin{array}{*{20}l} {frac{{text{r}}}{{0.9{text{ET}}_{{text{c}}} }}} hfill & {r < 0.9E{text{T}}_{{text{c}}} } hfill \ 1 hfill & {0.9E{text{T}}_{{text{c}}} le r le 1.2E{text{T}}_{{text{c}}} } hfill \ {frac{{1.2{text{ET}}_{{text{c}}} }}{{text{r}}}} hfill & {r > 1.2E{text{T}}_{{text{c}}} } hfill \ end{array} } right.$$
(7)
where Fi(r) is the water suitability of a certain growth period; r is the accumulated precipitation of peanut in a certain development period; ETc is the water demand of peanut in each growth period.
$${mathrm{ET}}_{mathrm{c}}={mathrm{K}}_{mathrm{c}}cdot {mathrm{ET}}_{0}$$
(8)
where Kc is the peanut crop coefficient (Table 2) and ET0 is the crop reference evapotranspiration, which is calculated by the Penman Monteith method recommended by the international food and Agriculture Organization (FAO).
Sunshine suitability model
Sunshine hours are an important condition for photosynthesis. The “light compensation point” and “light saturation point” of peanut are relatively high, and more sunshine hours are required for photosynthesis. Under certain conditions of water, temperature and carbon dioxide, photosynthesis increases or decreases with the increase or decrease of light. Relevant studies show that when the sunshine hours reach more than 55% of the available sunshine hours, the crops reach the appropriate state to reflect the light37. The following formula is used to calculate the sunshine suitability of peanut in each growth period.
$${mathrm{F}}_{mathrm{i}}left(mathrm{s}right)=left{begin{array}{l}frac{mathrm{S}}{{mathrm{S}}_{0}} quad S<{mathrm{S}}_{0}\ 1 quad S>{mathrm{S}}_{0}end{array}right.$$
(9)
where Fi(s) is the sunshine suitability of peanut in a certain development period, S is the actual sunshine hours in a certain growth period, S0 is 55% of the sunshine hours (L0), and the calculation method of L0 refers to the following formula.
$${mathrm{L}}_{0}=frac{2mathrm{t}}{15}$$
(10)
$$mathrm{sin}frac{mathrm{t}}{2}=sqrt{frac{mathrm{sin}(45^circ -frac{mathrm{varnothing }-updelta -upgamma }{2})times mathrm{sin}(45^circ +frac{mathrm{varnothing }-updelta -upgamma }{2})}{mathrm{cosvarnothing }times mathrm{cosdelta }}}$$
(11)
where Φ is the geographic latitude, δ is the declination, γ is the astronomical refraction, t is the angle.
Comprehensive suitability model
Peanut has different needs for meteorological elements such as temperature, sunshine and precipitation in different growth periods. In order to analyze the impact of meteorological factors in different growth periods on yield, correlation analysis was conducted between the suitability of temperature, precipitation and sunshine in each growth period and the relative meteorological yield of peanut, and the correlation coefficient of each growth period divided by the sum of the correlation coefficients of the whole growth period was used as the weight coefficient of the suitability of temperature, precipitation and sunshine in each growth period (Table 3). The climatic suitability of each single element in peanut growing season is calculated by using formulas (12) and (13):
$$left{begin{array}{c}{mathrm{b}}_{mathrm{ti}}=frac{{mathrm{a}}_{mathrm{ti}}}{sum_{mathrm{i}=1}^{mathrm{n}}{mathrm{a}}_{mathrm{ti}}}\ {mathrm{b}}_{mathrm{ri}}=frac{{mathrm{a}}_{mathrm{ri}}}{{sum }_{mathrm{i}=1}^{mathrm{n}}{mathrm{a}}_{mathrm{ri}}}\ {mathrm{b}}_{mathrm{si}}=frac{{mathrm{a}}_{mathrm{si}}}{{sum }_{mathrm{i}=1}^{mathrm{n}}{mathrm{a}}_{mathrm{si}}}end{array}right.$$
(12)
$$left{begin{array}{c}F(t)={sum }_{mathrm{i}=1}^{mathrm{n}}left[{mathrm{b}}_{mathrm{ti}}{mathrm{F}}_{mathrm{i}}(mathrm{t})right]\ F(r)={sum }_{mathrm{i}=1}^{mathrm{n}}left[{mathrm{b}}_{mathrm{ri}}{mathrm{F}}_{mathrm{i}}(mathrm{r})right]\ F(s)={sum }_{mathrm{i}=1}^{mathrm{n}}left[{mathrm{b}}_{mathrm{si}}{mathrm{F}}_{mathrm{i}}(mathrm{s})right]end{array}right.$$
(13)
where bti, bri and bsi are the weight coefficients of temperature, precipitation and sunshine suitability in the i growth period respectively, ati, ari and asi are the correlation coefficients between temperature, precipitation and sunshine suitability and meteorological impact index of peanut yield in the i growth period respectively, and F(t), F(r) and F(s) are the temperature, precipitation and sunshine suitability in peanut growth season respectively.
Then, the geometric average method is used to obtain the comprehensive suitability of peanut growth season, as shown in formula (14).
$$F(S)=sqrt[3]{F(t)times F(r)times F(s)}$$
(14)
Verification of climatic zoning results
Drought and flood disaster index
On the basis of previous studies, in view of the different water demand of peanut in different development stages, this paper adds the water demand of peanut in different development stages as an important index to calculate, and constructs a standardized precipitation crop water demand index (SPRI) that can comprehensively characterize the drought and flood situation of peanut, so as to judge and analyze the occurrence of drought and flood disasters of peanut.
Step 1: calculate the difference D between precipitation and crop water demand at each development stage
$${D}_{i}={P}_{i}-{ET}_{ci}$$
(15)
where Pi is the precipitation in the i development period (mm), and ETci is the crop water demand in the i development period (mm).
Step 2: normalize the data sequence.
Since there are negative values in the original sequence, it is necessary to normalize the data when calculating the standardized precipitation crop water demand index. The normalized value is the SPRI value. The normalization method and drought and flood classification are consistent with SPEI index38,39,40.
Chilling injury index
Based on the results of previous studies41, the abnormal percentage of caloric index was selected as the index of low-temperature chilling injury of peanut to judge and analyze the occurrence of chilling injury in different growth stages. The specific calculation process and formula are as follows:
Step 1: calculate the caloric index of different development stages.
Combined with the growth and development characteristics of peanut and considering the appropriate temperature, lower limit temperature and upper limit temperature at different growth stages of peanut, the caloric index can reflect the response of crops to environmental heat conditions. The average value of daily heat index is taken as the heat index of growth stage to reflect the influence of heat conditions in different growth stages on crop growth and development. Refer to formulas (5) and (6) to calculate the heat index Fi(t) at different development stages.
Step 2: calculate the percentage of heat index anomaly
$${I}_{ci}=frac{{F}_{i}(t)-overline{{F }_{i}(t)}}{overline{{F }_{i}(t)}}times 100%$$
(16)
where Ici is the Chilling injury index of stage i, Fi(t) is the heat index of stage i, and (overline{{F }_{i}(t)}) is the average value of the heat index of stage i over the years.
Heat injury index
Based on the results of previous studies42, taking the average temperature of 26 °C, 30 °C and 28 °C and the daily maximum temperature of 35 °C, 35 °C and 37 °C as the critical temperature index to identify the heat damage of peanut in three growth stages, if this condition is met and lasts for more than 3 days, it will be recorded as a high temperature event.
Disaster frequency
Disaster frequency (Pi) is defined as the ratio of the number of years of disaster at a certain station to the total number of years in the study period43, which is calculated by formula (17).
$${P}_{i}=frac{n}{N}times 100%$$
(17)
where n is the number of years of disaster events to some extent at a certain growth period at a certain station, and N is the total number of years.
[ad_2]
Source link